Introduction to Neural Network Architectures: Perceptrons, MLPs, and CNNs

Neural networks are at the heart of many modern artificial intelligence applications. Let's explore some fundamental building blocks and architectures.

The Basic Unit: The Perceptron

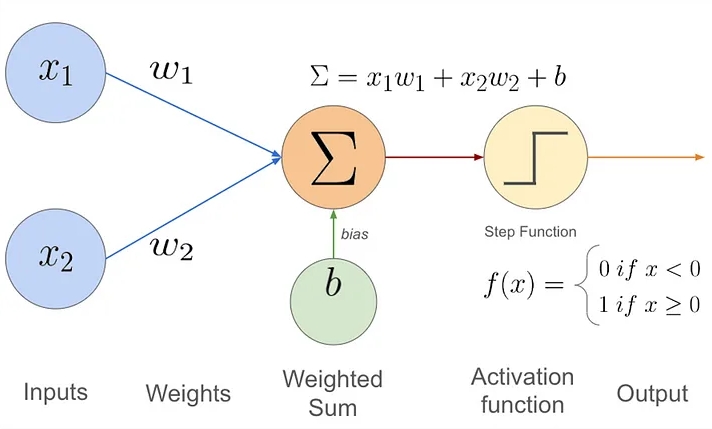
A unit (often referred to as a neuron or perceptron in simpler models) receives weighted signals from other units or inputs. It computes a weighted sum of these signals and then passes this sum through an activation function to produce an output.

Essentially, it's a linear classifier unit equipped with an activation function.

Figure 1: Components of an AND Gate Perceptron with Step Function. Reference from：Deep Learning 101: Lesson 7— Perceptron

Multilayer Perceptrons (MLPs)

Multilayer Perceptrons are a class of feedforward artificial neural networks. They consist of at least three layers of nodes.

Structure

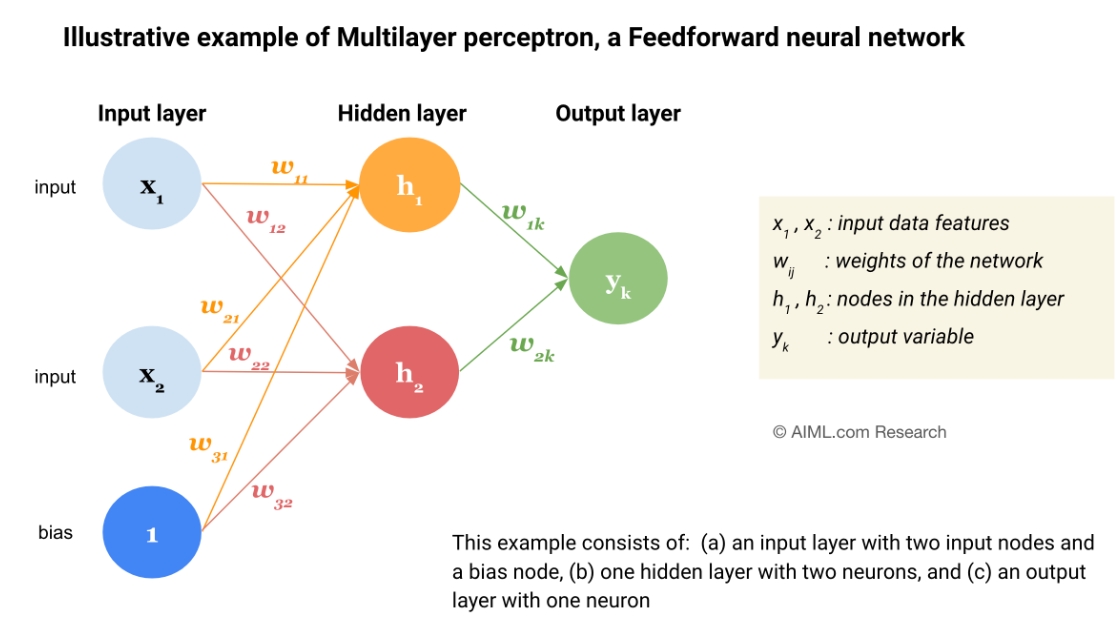
Illustrative example of Multilayer perceptron (MLP), a Feedforward neural network — Illustrative example of Multilayer perceptron (MLP), a feedforward neural network.
Source: What is a Multilayer Perceptron (MLP) or aFeedforward Neural Network (FNN)?What is a Multilayer Perceptron (MLP) or a Feedforward Neural Network (FNN)? (AIML.com)

Input Layer: Receives the initial data or features.
Hidden Layer(s): One or more layers between the input and output layers. These layers perform intermediate computations and enable the network to learn complex patterns.
Output Layer: Produces the final result of the network (e.g., classification or regression values).

Forward Propagation / Forward Evaluation

This is the process by which input data is fed through the network to generate an output.

Computation starts from the input layer and proceeds layer by layer towards the output layer.
Each unit in a layer calculates a weighted sum of its inputs from the preceding layer.
An activation function is applied to this sum to produce the unit's output, also known as its activation value.
This output then serves as input to the units in the next layer.

Backpropagation Algorithm

The Backpropagation Algorithm is the standard method for training MLPs. It's used to efficiently compute the gradient of the loss function with respect to the network's weights, allowing the weights to be learned.

Forward Propagation: The input data is passed through the network to compute the output and the resulting error (e.g., the difference between the predicted output and the actual target value).
Compute Error ( $\Delta$ ): The error at the output layer is calculated.
Backward Pass: The error ( $\Delta$ ) is propagated backward from the output layer through the hidden layers. The gradient of the error with respect to each weight is calculated.
Update Weights: An optimization algorithm, such as Gradient Descent, uses these gradients to update the weights in the network to minimize the error.

Convolutional Neural Networks (CNNs)

Convolutional Neural Networks are a specialized type of neural network designed to process data with a grid-like topology, such as images. They are highly effective for tasks like image recognition, object detection, and image segmentation.

Structure

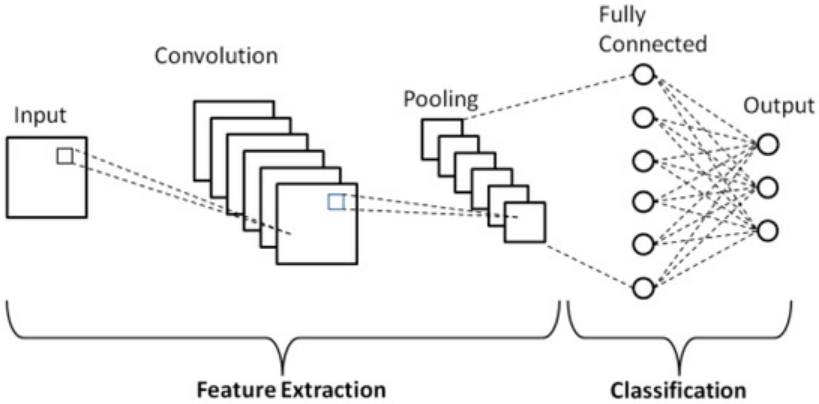
Schematic diagram of a basic CNN architecture — Figure 1. Schematic diagram of a basic convolutional neural network (CNN) architecture.
From: Phung, V.H.; Rhee, E.J. A Deep Learning Approach for Classification of Cloud Image Patches on Small Datasets. *J. Inf. Commun. Converg. Eng.* **2018**, 16, 173–178. (Google Scholar; CrossRef)

CNNs typically consist of several types of layers:

Convolutional Layers (CONV)
- Connected to a local region of the input, known as the receptive field.
- Employ a set of learnable filters (or kernels).
  - Each filter slides (or convolves) across the input data. The convolution operation involves computing the dot product between the filter weights and the input values within the receptive field, and then adding a bias term.
  - This process detects specific local features (e.g., edges, textures, motifs) and produces a 2D feature map (or activation map) for each filter.
Activation Layer
- Applies an element-wise non-linear transformation to the output feature maps from the convolutional layer.
- Commonly used activation functions include:
  - ReLU (Rectified Linear Unit): $\text{ReLU}(x) = \max(0, x)$ . It introduces non-linearity and helps with issues like vanishing gradients.
  - Sigmoid Function: $\sigma(z) = \frac{1}{1 + e^{-z}}$ . Often used in older CNNs or for binary classification output layers.
Pooling Layers (POOL)
- Perform down-sampling on the feature maps, reducing their spatial dimensions (width and height) while keeping the depth (number of feature maps) unchanged.
- Benefits:
  - Reduces the computational load and the number of parameters in subsequent layers.
  - Provides a degree of translation invariance (small shifts in the input don't drastically change the output).
  - Helps prevent overfitting.
- Max Pooling is a common type: A window slides over the input feature map, and for each window, the maximum value is selected as the output.
Fully Connected Layers (FC)
- These layers typically form the final part of a CNN.
- Neurons in a fully connected layer have connections to all activations in the previous layer, similar to traditional MLPs.
- They integrate the high-level features learned by the preceding convolutional and pooling layers to perform the final classification or regression task.